Note
Click here to download the full example code
Uniform triangle¶
Test and validation of potential of uniformaly distributed charge density
- For the math see:
A. S. Ferguson, Xu Zhang and G. Stroink, “A complete linear discretization for calculating the magnetic field using the boundary element method,” in IEEE Transactions on Biomedical Engineering, vol. 41, no. 5, pp. 455-460, May 1994. doi: 10.1109/10.293220
import numpy as np
import matplotlib.pyplot as plt
import sys
from mayavi import mlab
path = "/m/home/home8/80/makinea1/unix/pythonstuff/bfieldtools"
if path not in sys.path:
sys.path.insert(0, path)
from bfieldtools.integrals import triangle_potential_uniform
from bfieldtools.utils import tri_normals_and_areas
%% Test potential shape slightly above the surface
points = np.array([[0, 0, 0], [1, 0, 0], [0, 1, 0]])
tris = np.array([[0, 1, 2]])
p_tris = points[tris]
# Evaluation points
Nx = 100
xx = np.linspace(-2, 2, Nx)
X, Y = np.meshgrid(xx, xx, indexing="ij")
Z = np.zeros_like(X) + 0.01
p_eval = np.array([X, Y, Z]).reshape(3, -1).T
# Difference vectors
RR = p_eval[:, None, None, :] - p_tris[None, :, :, :]
tn, ta = tri_normals_and_areas(points, tris)
pot = triangle_potential_uniform(RR, tn, False)
# Plot shape
plt.figure()
plt.imshow(pot[:, 0].reshape(Nx, Nx), extent=(xx.min(), xx.max(), xx.max(), xx.min()))
plt.ylabel("x")
plt.xlabel("y")
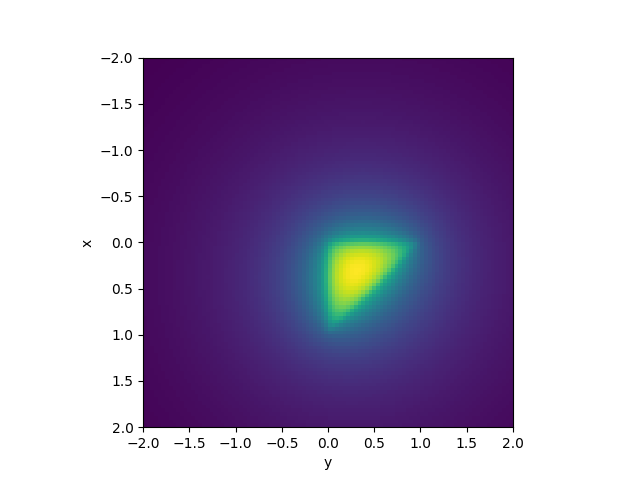
Out:
Text(0.5, 0, 'y')
- %% Test asymptotic behavour by comparing potential of charge at the
center of mass of the triangle having the same first moment
def charge_potential(Reval, Rcharge, moment):
R = Reval - Rcharge
r = np.linalg.norm(R, axis=1)
return moment / r
# Center of mass
Rcharge = points.mean(axis=0)
# Moment
m = ta
# Eval points
Neval = 100
cases = np.arange(3)
f, ax = plt.subplots(1, 3)
mlab.figure(bgcolor=(1, 1, 1))
mlab.triangular_mesh(*points.T, tris, color=(0.5, 0.5, 0.5))
for c in cases:
p_eval2 = np.zeros((Neval, 3))
if c == 0:
z = np.linspace(0.01, 20, Neval)
p_eval2[:, 2] = z
p_eval2 += Rcharge
mlab.points3d(*p_eval2.T, color=(1, 0, 0), scale_factor=0.1)
lab = "z"
elif c == 1:
x = np.linspace(0.01, 20, Neval)
p_eval2[:, 0] = x
mlab.points3d(*p_eval2.T, color=(0, 1, 0), scale_factor=0.1)
lab = "x"
elif c == 2:
y = np.linspace(0.01, 20, Neval)
p_eval2[:, 1] = y
mlab.points3d(*p_eval2.T, color=(0, 0, 1), scale_factor=0.1)
lab = "y"
plt.sca(ax[c])
# Plot dipole field approximating uniform dipolar density
plt.semilogy(z, charge_potential(p_eval2, Rcharge, m))
# Plot sum of the linear dipoles
RR = p_eval2[:, None, None, :] - p_tris[None, :, :, :]
pot = triangle_potential_uniform(RR, tn, False)
plt.semilogy(z, pot)
plt.xlabel(lab)
if c == 0:
plt.ylabel("potential")
if c == 2:
plt.legend(("Approx.", "True"))
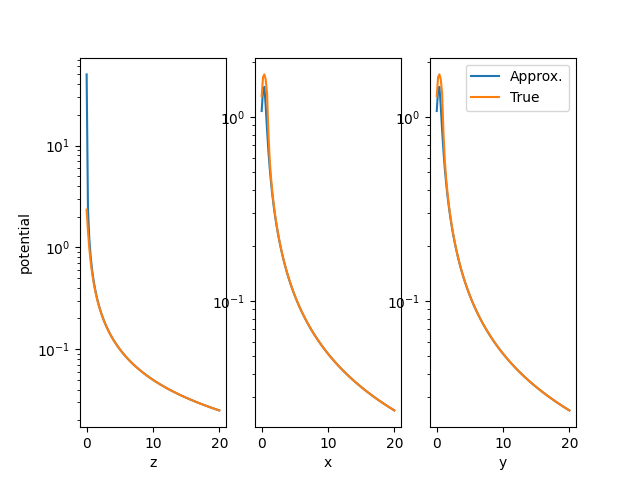

Total running time of the script: ( 0 minutes 1.345 seconds)
Estimated memory usage: 9 MB
