Note
Click here to download the full example code
MAMBA coil¶
Compact example of a biplanar coil producing homogeneous field in a number of target regions arranged in a grid. Meant to demonstrate the flexibility in target choice, inspired by the technique “multiple-acquisition micro B(0) array” (MAMBA) technique, see https://doi.org/10.1002/mrm.10464
import numpy as np
from mayavi import mlab
import trimesh
from bfieldtools.mesh_conductor import MeshConductor
from bfieldtools.coil_optimize import optimize_streamfunctions
from bfieldtools.contour import scalar_contour
from bfieldtools.viz import plot_3d_current_loops
from bfieldtools.utils import combine_meshes, load_example_mesh
# Load simple plane mesh that is centered on the origin
planemesh = load_example_mesh("10x10_plane_hires")
# Specify coil plane geometry
center_offset = np.array([0, 0, 0])
standoff = np.array([0, 1.5, 0])
# Create coil plane pairs
coil_plus = trimesh.Trimesh(
planemesh.vertices + center_offset + standoff, planemesh.faces, process=False
)
coil_minus = trimesh.Trimesh(
planemesh.vertices + center_offset - standoff, planemesh.faces, process=False
)
joined_planes = combine_meshes((coil_plus, coil_minus))
# Create mesh class object
coil = MeshConductor(mesh_obj=joined_planes, fix_normals=True, basis_name="inner")
Set up target and stray field points. Here, the target points are on a planar 4x4 grid slightly smaller than the coil dimensions.
center = np.array([0, 0, 0])
sidelength = 0.5
n = 4
height = 0.1
n_height = 2
xx = np.linspace(-sidelength / 2, sidelength / 2, n)
yy = np.linspace(-height / 2, height / 2, n_height)
zz = np.linspace(-sidelength / 2, sidelength / 2, n)
X, Y, Z = np.meshgrid(xx, yy, zz, indexing="ij")
x = X.ravel()
y = Y.ravel()
z = Z.ravel()
target_points = np.array([x, y, z]).T
grid_target_points = list()
target_field = list()
hori_offsets = [-3, -1, 1, 3]
vert_offsets = [-3, -1, 1, 3]
for i, offset_x in enumerate(hori_offsets):
for j, offset_y in enumerate(vert_offsets):
grid_target_points.append(target_points + np.array([offset_x, 0, offset_y]))
target_field.append((i + j - 3) * np.ones((len(target_points),)))
target_points = np.asarray(grid_target_points).reshape((-1, 3))
target_field = np.asarray(target_field).reshape((-1,))
target_field = np.array(
[np.zeros((len(target_field),)), target_field, np.zeros((len(target_field),))]
).T
target_abs_error = np.zeros_like(target_field)
target_abs_error[:, 1] += 0.1
target_abs_error[:, 0::2] += 0.1
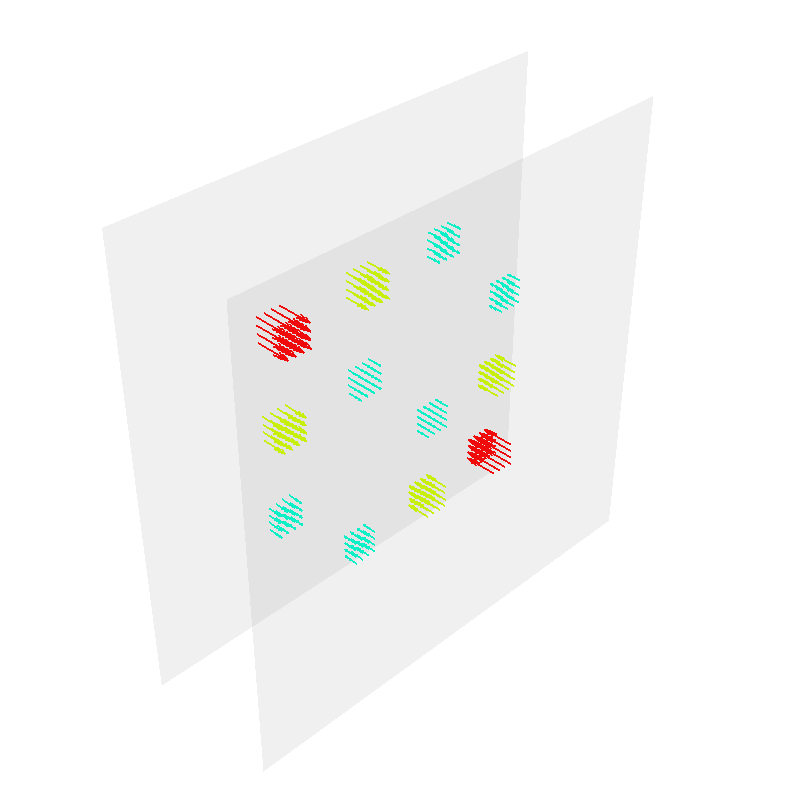
Plot target points and mesh
coil.plot_mesh(opacity=0.1)
mlab.quiver3d(*target_points.T, *target_field.T)
Out:
<mayavi.modules.vectors.Vectors object at 0x7f0c11cf0590>
Compute coupling matrix that is used to compute the generated magnetic field, create field specification
target_spec = {
"coupling": coil.B_coupling(target_points),
"abs_error": target_abs_error,
"target": target_field,
}
Out:
Computing magnetic field coupling matrix, 3184 vertices by 512 target points... took 0.57 seconds.
Run QP solver, plot result
import mosek
coil.s, prob = optimize_streamfunctions(
coil,
[target_spec],
objective="minimum_inductive_energy",
solver="MOSEK",
solver_opts={"mosek_params": {mosek.iparam.num_threads: 8}},
)
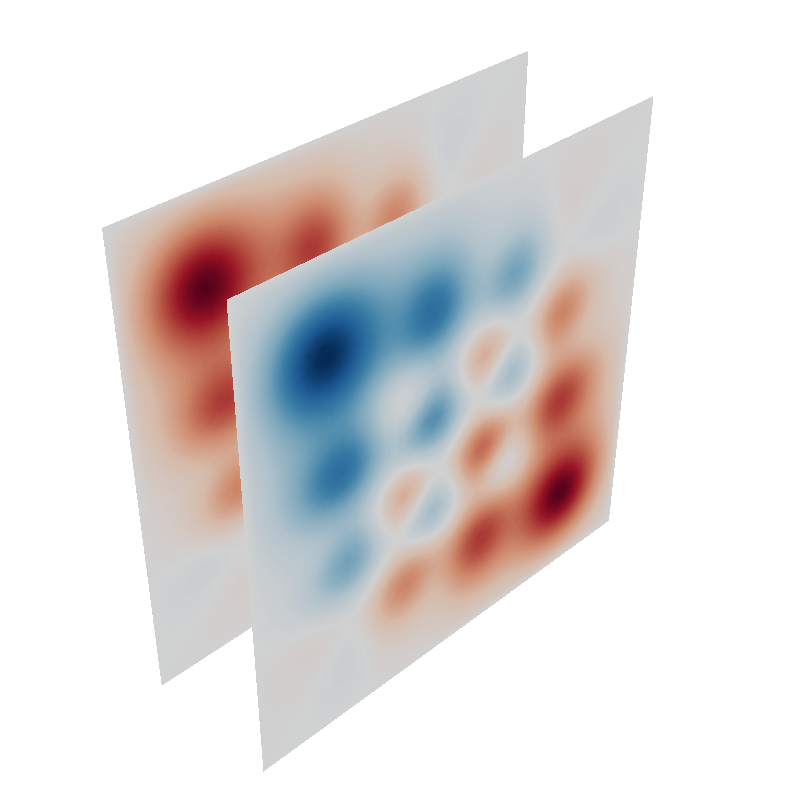
coil.s.plot()
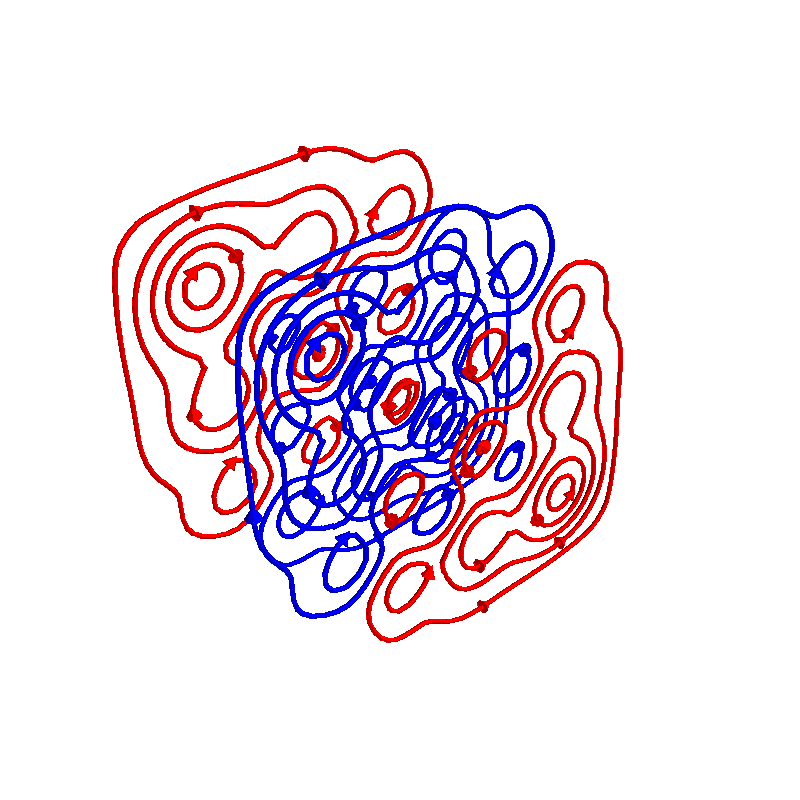
coil.s.discretize(N_contours=10).plot_loops()
Out:
Computing the inductance matrix...
Computing self-inductance matrix using rough quadrature (degree=2). For higher accuracy, set quad_degree to 4 or more.
Estimating 34964 MiB required for 3184 by 3184 vertices...
Computing inductance matrix in 80 chunks (9273 MiB memory free), when approx_far=True using more chunks is faster...
Computing triangle-coupling matrix
Inductance matrix computation took 14.08 seconds.
Pre-existing problem not passed, creating...
Passing parameters to problem...
Passing problem to solver...
Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 5970
Cones : 1
Scalar variables : 5795
Matrix variables : 0
Integer variables : 0
Optimizer started.
Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 5970
Cones : 1
Scalar variables : 5795
Matrix variables : 0
Integer variables : 0
Optimizer - threads : 8
Optimizer - solved problem : the dual
Optimizer - Constraints : 2897
Optimizer - Cones : 1
Optimizer - Scalar variables : 5970 conic : 2898
Optimizer - Semi-definite variables: 0 scalarized : 0
Factor - setup time : 1.06 dense det. time : 0.00
Factor - ML order time : 0.20 GP order time : 0.00
Factor - nonzeros before factor : 4.20e+06 after factor : 4.20e+06
Factor - dense dim. : 0 flops : 2.91e+10
ITE PFEAS DFEAS GFEAS PRSTATUS POBJ DOBJ MU TIME
0 2.0e+02 1.0e+00 2.0e+00 0.00e+00 0.000000000e+00 -1.000000000e+00 1.0e+00 3.98
1 7.5e+01 3.8e-01 1.1e+00 -8.29e-01 1.092527523e+01 1.122576890e+01 3.8e-01 4.73
2 1.4e+01 7.0e-02 2.7e-01 -5.83e-01 1.310063162e+02 1.338387135e+02 7.0e-02 5.42
3 4.9e-01 2.5e-03 5.1e-03 1.88e-01 2.176256409e+02 2.186500663e+02 2.5e-03 6.06
4 1.0e-01 5.3e-04 3.6e-04 9.63e-01 1.601982077e+02 1.603056738e+02 5.3e-04 6.77
5 8.8e-03 4.4e-05 6.0e-06 9.92e-01 1.504225631e+02 1.504261347e+02 4.4e-05 7.43
6 3.6e-03 1.8e-05 1.6e-06 9.99e-01 1.496646785e+02 1.496661966e+02 1.8e-05 8.15
7 5.0e-04 2.5e-06 8.5e-08 1.00e+00 1.494005013e+02 1.494007311e+02 2.5e-06 8.89
8 2.5e-04 1.3e-06 3.0e-08 1.00e+00 1.493866996e+02 1.493868138e+02 1.3e-06 9.52
9 4.0e-05 2.0e-07 1.9e-09 1.00e+00 1.493759608e+02 1.493759792e+02 2.0e-07 10.14
10 4.8e-06 2.4e-08 8.1e-11 1.00e+00 1.493742426e+02 1.493742448e+02 2.4e-08 10.92
11 7.9e-08 8.7e-11 6.6e-13 1.00e+00 1.493740288e+02 1.493740285e+02 6.2e-12 11.69
Optimizer terminated. Time: 11.95
Interior-point solution summary
Problem status : PRIMAL_AND_DUAL_FEASIBLE
Solution status : OPTIMAL
Primal. obj: 1.4937402879e+02 nrm: 3e+02 Viol. con: 2e-10 var: 0e+00 cones: 0e+00
Dual. obj: 1.4937402853e+02 nrm: 7e+01 Viol. con: 3e-09 var: 1e-09 cones: 0e+00
<mayavi.core.scene.Scene object at 0x7f0c11d5cc50>
Total running time of the script: ( 0 minutes 41.531 seconds)
Estimated memory usage: 2569 MB