Note
Click here to download the full example code
Spherical harmonics-generating coil design¶
Example showing a basic biplanar coil producing a field profile defined by spherical harmonics. We use the surface harmonics basis for the stream function, and optimize the coupling to spherical harmonics components, thus creating a compact optimization problem that can be solved very quickly.
import numpy as np
import trimesh
from bfieldtools.mesh_conductor import MeshConductor
from bfieldtools.coil_optimize import optimize_streamfunctions
from bfieldtools.utils import combine_meshes, load_example_mesh
# Load simple plane mesh that is centered on the origin
planemesh = load_example_mesh("10x10_plane_hires")
# Specify coil plane geometry
center_offset = np.array([0, 0, 0])
standoff = np.array([0, 15, 0])
# Create coil plane pairs
coil_plus = trimesh.Trimesh(
planemesh.vertices + center_offset + standoff, planemesh.faces, process=False
)
coil_minus = trimesh.Trimesh(
planemesh.vertices + center_offset - standoff, planemesh.faces, process=False
)
joined_planes = combine_meshes((coil_plus, coil_minus))
# To spice things up, let's distort the planes a bit
joined_planes.vertices = (
joined_planes.vertices
- 0.5
* np.linalg.norm(joined_planes.vertices, axis=1)[:, None]
* np.sign(joined_planes.vertices[:, 1])[:, None]
* joined_planes.vertex_normals
)
joined_planes.vertices = (
joined_planes.vertices
- 0.5
* np.linalg.norm(joined_planes.vertices, axis=1)[:, None]
* np.sign(joined_planes.vertices[:, 1])[:, None]
* joined_planes.vertex_normals
)
# Create mesh class object
coil = MeshConductor(
mesh_obj=joined_planes,
fix_normals=True,
basis_name="suh",
N_suh=100,
sph_radius=0.2,
sph_normalization="energy",
)
Out:
Calculating surface harmonics expansion...
Computing the laplacian matrix...
Computing the mass matrix...
Set up target spherical harmonics components
target_alms = np.zeros((coil.opts["N_sph"] * (coil.opts["N_sph"] + 2),))
target_blms = np.zeros((coil.opts["N_sph"] * (coil.opts["N_sph"] + 2),))
target_blms[4] += 1
Create bfield specifications used when optimizing the coil geometry
target_spec = {
"coupling": coil.sph_couplings[1],
"abs_error": 0.01,
"target": target_blms,
}
Out:
Computing coupling matrices
l = 1 computed
l = 2 computed
l = 3 computed
l = 4 computed
l = 5 computed
Run QP solver
import mosek
coil.s, prob = optimize_streamfunctions(
coil,
[target_spec],
objective="minimum_ohmic_power",
solver="MOSEK",
solver_opts={"mosek_params": {mosek.iparam.num_threads: 8}},
)
Out:
Computing the resistance matrix...
Pre-existing problem not passed, creating...
Passing parameters to problem...
Passing problem to solver...
Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 172
Cones : 1
Scalar variables : 203
Matrix variables : 0
Integer variables : 0
Optimizer started.
Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 172
Cones : 1
Scalar variables : 203
Matrix variables : 0
Integer variables : 0
Optimizer - threads : 8
Optimizer - solved problem : the primal
Optimizer - Constraints : 21
Optimizer - Cones : 1
Optimizer - Scalar variables : 122 conic : 102
Optimizer - Semi-definite variables: 0 scalarized : 0
Factor - setup time : 0.00 dense det. time : 0.00
Factor - ML order time : 0.00 GP order time : 0.00
Factor - nonzeros before factor : 231 after factor : 231
Factor - dense dim. : 0 flops : 4.57e+04
ITE PFEAS DFEAS GFEAS PRSTATUS POBJ DOBJ MU TIME
0 2.6e+03 1.0e+00 1.0e+00 0.00e+00 5.000000000e-01 5.000000000e-01 1.0e+00 0.00
1 3.5e+02 1.3e-01 3.6e-01 -9.99e-01 2.106776004e+00 8.539033584e+00 1.3e-01 0.00
2 5.9e+01 2.2e-02 1.4e-01 -9.86e-01 1.056154434e+01 5.043072723e+01 2.2e-02 0.01
3 7.2e+00 2.7e-03 3.9e-02 -8.86e-01 5.862068212e+01 2.665291713e+02 2.7e-03 0.01
4 9.5e-01 3.6e-04 4.7e-03 -1.93e-01 7.820100570e+01 2.457313707e+02 3.6e-04 0.01
5 7.1e-02 2.7e-05 8.2e-05 8.62e-01 1.581261876e+01 2.492473364e+01 2.7e-05 0.01
6 3.1e-03 1.2e-06 6.1e-07 1.12e+00 1.293685796e+01 1.320298909e+01 1.2e-06 0.01
7 2.7e-04 1.0e-07 1.5e-08 1.10e+00 1.268464223e+01 1.270457442e+01 1.0e-07 0.01
8 7.9e-07 3.0e-10 2.1e-12 1.01e+00 1.260896786e+01 1.260901454e+01 3.0e-10 0.01
9 5.5e-10 2.8e-13 8.2e-18 1.00e+00 1.260893219e+01 1.260893222e+01 2.1e-13 0.01
Optimizer terminated. Time: 0.01
Interior-point solution summary
Problem status : PRIMAL_AND_DUAL_FEASIBLE
Solution status : OPTIMAL
Primal. obj: 1.2608932191e+01 nrm: 3e+01 Viol. con: 1e-10 var: 0e+00 cones: 0e+00
Dual. obj: 1.2608932224e+01 nrm: 3e+01 Viol. con: 2e-05 var: 1e-11 cones: 0e+00
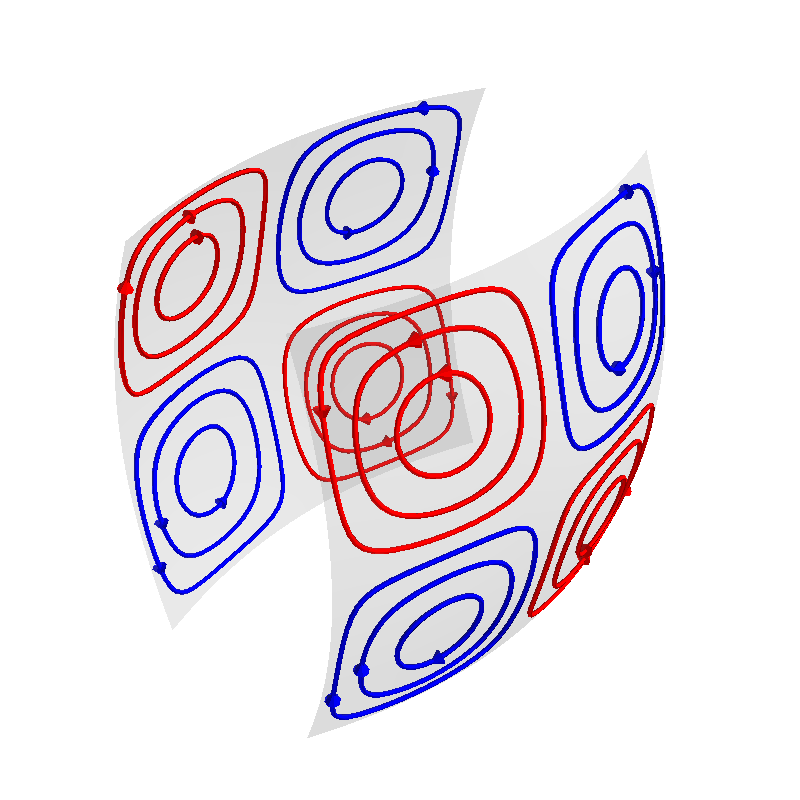
Plot coil windings
f = coil.plot_mesh(opacity=0.2)
loops = coil.s.discretize(N_contours=6)
loops.plot_loops(figure=f)
Out:
<mayavi.core.scene.Scene object at 0x7fa450fab8f0>
Now, let’s change the spherical harmonics inner expansion radius (i.e. the target region radius) and optimize a new coil (with the same target sph component)
coil.set_sph_options(sph_radius=1.4)
target_spec = {
"coupling": coil.sph_couplings[1],
"abs_error": 0.01,
"target": target_blms,
}
Out:
Computing coupling matrices
l = 1 computed
l = 2 computed
l = 3 computed
l = 4 computed
l = 5 computed
Run QP solver
import mosek
coil.s2, prob = optimize_streamfunctions(
coil,
[target_spec],
objective="minimum_ohmic_power",
solver="MOSEK",
solver_opts={"mosek_params": {mosek.iparam.num_threads: 8}},
)
Out:
Pre-existing problem not passed, creating...
Passing parameters to problem...
Passing problem to solver...
Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 172
Cones : 1
Scalar variables : 203
Matrix variables : 0
Integer variables : 0
Optimizer started.
Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 172
Cones : 1
Scalar variables : 203
Matrix variables : 0
Integer variables : 0
Optimizer - threads : 8
Optimizer - solved problem : the primal
Optimizer - Constraints : 21
Optimizer - Cones : 1
Optimizer - Scalar variables : 122 conic : 102
Optimizer - Semi-definite variables: 0 scalarized : 0
Factor - setup time : 0.00 dense det. time : 0.00
Factor - ML order time : 0.00 GP order time : 0.00
Factor - nonzeros before factor : 231 after factor : 231
Factor - dense dim. : 0 flops : 4.58e+04
ITE PFEAS DFEAS GFEAS PRSTATUS POBJ DOBJ MU TIME
0 2.0e+00 1.0e+00 1.0e+00 0.00e+00 5.000000000e-01 5.000000000e-01 1.0e+00 0.00
1 6.7e-01 3.3e-01 1.8e-01 1.14e+00 3.511690623e-01 3.232903157e-01 3.3e-01 0.01
2 2.5e-01 1.3e-01 1.9e-02 9.73e-01 1.001501457e+00 9.333696466e-01 1.3e-01 0.01
3 3.9e-02 2.0e-02 6.8e-04 1.31e+00 1.073643030e+00 1.063449217e+00 2.0e-02 0.01
4 4.2e-03 2.1e-03 2.2e-05 1.32e+00 1.085794962e+00 1.084873799e+00 2.1e-03 0.01
5 7.5e-05 3.8e-05 4.8e-08 1.21e+00 1.088222840e+00 1.088208156e+00 3.8e-05 0.01
6 1.5e-07 7.5e-08 4.3e-12 1.01e+00 1.088267709e+00 1.088267680e+00 7.5e-08 0.01
7 5.8e-10 1.4e-10 1.2e-15 1.00e+00 1.088267811e+00 1.088267811e+00 2.9e-10 0.01
Optimizer terminated. Time: 0.01
Interior-point solution summary
Problem status : PRIMAL_AND_DUAL_FEASIBLE
Solution status : OPTIMAL
Primal. obj: 1.0882678108e+00 nrm: 4e+00 Viol. con: 2e-10 var: 0e+00 cones: 0e+00
Dual. obj: 1.0882678106e+00 nrm: 9e+00 Viol. con: 2e-08 var: 6e-11 cones: 0e+00
Plot coil windings
f2 = coil.plot_mesh(opacity=0.2)
loops2 = coil.s2.discretize(N_contours=6)
loops2.plot_loops(figure=f2)

Out:
<mayavi.core.scene.Scene object at 0x7fa4369149b0>
Total running time of the script: ( 0 minutes 46.518 seconds)
Estimated memory usage: 262 MB
