Note
Click here to download the full example code
Solving linearly polarizing material in a homogenenous fieldΒΆ
The example is based on the following integral equation of a piecewise harmonic potential \(U\) on the boundary of the polarizing material
\[\frac{\mu_0 + \mu}{2} U(\vec{r}) = \mu_0 U_\infty(\vec{r}) + \frac{\mu_0 - \mu}{4\pi}\int_{S} U(\vec{r}\,') (\hat{n}' \cdot \nabla') \frac{1}{|\vec{r}-\vec{r}\,'|} dS'\,.\]
\(U\) is the magnetic scalar potential to be solved
\(\mu_0\) is the permeability of the free space
\(\mu\) is the permeability of the material
\(U_\infty\) is the magnetic scalar potential without the material
\(S\) is the surface of the material
After discretization \(U(\vec{r})=\sum_n u_n h_n(\vec{r})\) and integrating the integral equation over every hat \(h_n(\vec{r})\), a linear system of equations is obtained
\[\mathbf{N}\mathbf{u} = \frac{2}{1+\mu_\mathrm{r}} \mathbf{u}_\infty + \frac{1 - \mu_\mathrm{r}}{4\pi(1 + \mu_\mathrm{r})}\mathbf{D}\mathbf{u}\,.\]
\(\mathbf{u}\) is \(U\) at the mesh nodes
\(\mathbf{u}_\infty\) is the potential \(U_\infty\) integrated over hat functions
\(\mu_\mathrm{r}\) is the relative permeability of the material
\(\mathbf{D}\) is the double-layer coupling matrix
\(\mathbf{N}\) is the mesh mass matrix
import numpy as np
import matplotlib.pyplot as plt
from mayavi import mlab
from bfieldtools.mesh_conductor import MeshConductor as Conductor
from bfieldtools.mesh_magnetics import magnetic_field_coupling
from bfieldtools.mesh_magnetics import scalar_potential_coupling
from bfieldtools.mesh_calculus import mass_matrix
from bfieldtools.utils import load_example_mesh
from trimesh.creation import icosphere
# Use a sphere
# mesh = icosphere(3, 1)
# Use a cube
mesh = load_example_mesh("cube")
mesh.vertices -= mesh.vertices.mean(axis=0)
mesh.apply_scale(0.2)
def Dmatrix(mesh1, mesh2, Nchunks=100):
"""
"Double-layer potential" coupling between two meshes
using a Galerkin method with hat basis
Discretize integral equations using hat functions
on on both meshes. Potential from mesh1 hat functions
is calculated analytically and integrated over the
hat functions of mesh2 numerically
Parameters
----------
mesh1 : Trimesh object
mesh2 : Trimesh object
Nchunks : int, optional
Number of chunks in the potential calculation. The default is 100.
Returns
-------
None.
"""
face_points = mesh2.vertices[mesh2.faces]
weights = np.array([[0.5, 0.25, 0.25], [0.25, 0.5, 0.25], [0.25, 0.25, 0.5]])
# Combine vertices for quadrature points
Rquad = np.einsum("...ij,ik->...kj", face_points, weights)
R = Rquad.reshape(-1, 3)
U = scalar_potential_coupling(
mesh1, R, Nchunks, multiply_coeff=False, approx_far=True
)
face_areas = mesh2.area_faces
# Reshape and multiply by quadrature weights
Dcomps = U.reshape(Rquad.shape[:2] + (len(mesh2.vertices),)) * (
face_areas[:, None, None] / 3
)
# Sum up the quadrature points
D = mesh2.faces_sparse @ Dcomps[:, 0, :]
D += mesh2.faces_sparse @ Dcomps[:, 1, :]
D += mesh2.faces_sparse @ Dcomps[:, 2, :]
if mesh1 is mesh2:
# Recalculate diagonals
d = np.diag(D)
D -= np.diag(d)
# Make rows sum to -2*pi*(vertex area), should be more accurate
d2 = -2 * np.pi * mass_matrix(mesh2, lumped=False) - np.diag(D.sum(axis=1))
D += d2
# Make D solvable by adding rank-1 matrix
D += np.ones_like(D) * np.max(np.linalg.svd(D, False, False)) / D.shape[1]
return D
# Some linear input potentials -> uniform field
def phi0x(r):
return r[:, 0]
def phi0y(r):
return r[:, 1]
def phi0z(r):
return r[:, 2]
def project_to_hats(mesh, func):
"""
Numerically integrate func over hat functions
Parameters
----------
mesh : Trimesh object
the domain for hat functions
func : function
potential function for phi0, takes (N,3) array
of points as input
Returns
-------
p_mat : (Nvertices,) array
func projected on the hat functions
"""
# Index vertex points for each faces
face_points = mesh.vertices[mesh.faces]
weights = np.array([[0.5, 0.25, 0.25], [0.25, 0.5, 0.25], [0.25, 0.25, 0.5]])
# Combine vertices for quadrature points
Rquad = np.einsum("...ij,ik->...kj", face_points, weights)
R = Rquad.reshape(-1, 3)
# Evaluation func at quadrature points
p = func(R)
face_areas = mesh.area_faces
# Reshape and multiply by quadrature weights
pcomps = p.reshape(Rquad.shape[:2]) * (face_areas[:, None] / 3)
# Sum up the quadrature points
p_mat = mesh.faces_sparse @ pcomps[:, 0]
p_mat += mesh.faces_sparse @ pcomps[:, 1]
p_mat += mesh.faces_sparse @ pcomps[:, 2]
return p_mat
Out:
Computing D matrix
Computing scalar potential coupling matrix, 2348 vertices by 14076 target points... took 11.79 seconds.
Computing mass matrix
print("Computing input potential")
pp = project_to_hats(mesh, phi0x)
mu_r = 100
c1 = (1 - mu_r) / (1 + mu_r)
u = np.linalg.solve(M - 1 / (2 * np.pi) * c1 * D, -2 * pp / (mu_r + 1))
# Plot potential on the mesh
mlab.figure("Potential on the boundary", bgcolor=(1, 1, 1))
m = mlab.triangular_mesh(*mesh.vertices.T, mesh.faces, scalars=u, colormap="bwr")
m.actor.mapper.interpolate_scalars_before_mapping = True
m.module_manager.scalar_lut_manager.number_of_colors = 32
Out:
Computing input potential
Load plane for the visualization of the potential
plane = load_example_mesh("10x10_plane_hires", process=True)
t = np.eye(4)
t[1:3, 1:3] = np.array([[0, 1], [-1, 0]])
plane.apply_transform(t)
plane.apply_scale(0.3)
plane = plane.subdivide()
Uplane = scalar_potential_coupling(
mesh, plane.vertices, multiply_coeff=False, approx_far=True
)
uprim = phi0x(plane.vertices)
usec = (mu_r - 1) / (4 * np.pi) * Uplane @ u
uplane = uprim + usec
# Meshgrid on the same plane for the bfield
X, Y = np.meshgrid(
np.linspace(-1.5, 1.5, 50), np.linspace(-1.5, 1.5, 50), indexing="ij"
)
pp = np.zeros((50 * 50, 3))
pp[:, 0] = X.flatten()
pp[:, 1] = Y.flatten()
Bplane = magnetic_field_coupling(mesh, pp, analytic=True)
bprim = pp * 0 # copy pp
# add x directional field
mu0 = 1e-7 * 4 * np.pi
bprim[:, 0] = -1
# In this simulation mu0==1 is assumed
# magnetic_field_coupling uses mu0 in SI units
bplane = (mu_r - 1) / (4 * np.pi) / mu0 * Bplane @ u + bprim
# uplane[Uplane.sum(axis=1)]
Out:
Computing scalar potential coupling matrix, 2348 vertices by 6221 target points... took 4.16 seconds.
Computing magnetic field coupling matrix analytically, 2348 vertices by 2500 target points... took 7.62 seconds.
mlab.figure("Potential for B", bgcolor=(1, 1, 1), size=(1000, 1000))
m = mlab.triangular_mesh(*plane.vertices.T, plane.faces, scalars=uplane, colormap="bwr")
m.actor.mapper.interpolate_scalars_before_mapping = True
m.module_manager.scalar_lut_manager.number_of_colors = 32
# vectors = mlab.quiver3d(*(plane.triangles_center + np.array([0,0,0.001])).T,
# *(-gradient(uplane, plane)), color=(0,0,0),
# scale_mode='none', scale_factor=0.01, mode='arrow')
# vectors.glyph.mask_input_points = True
# vectors.glyph.mask_points.random_mode_type = 0
# vectors.glyph.mask_points.on_ratio = 4
# vectors.glyph.glyph_source.glyph_position = 'center'
m.scene.z_plus_view()
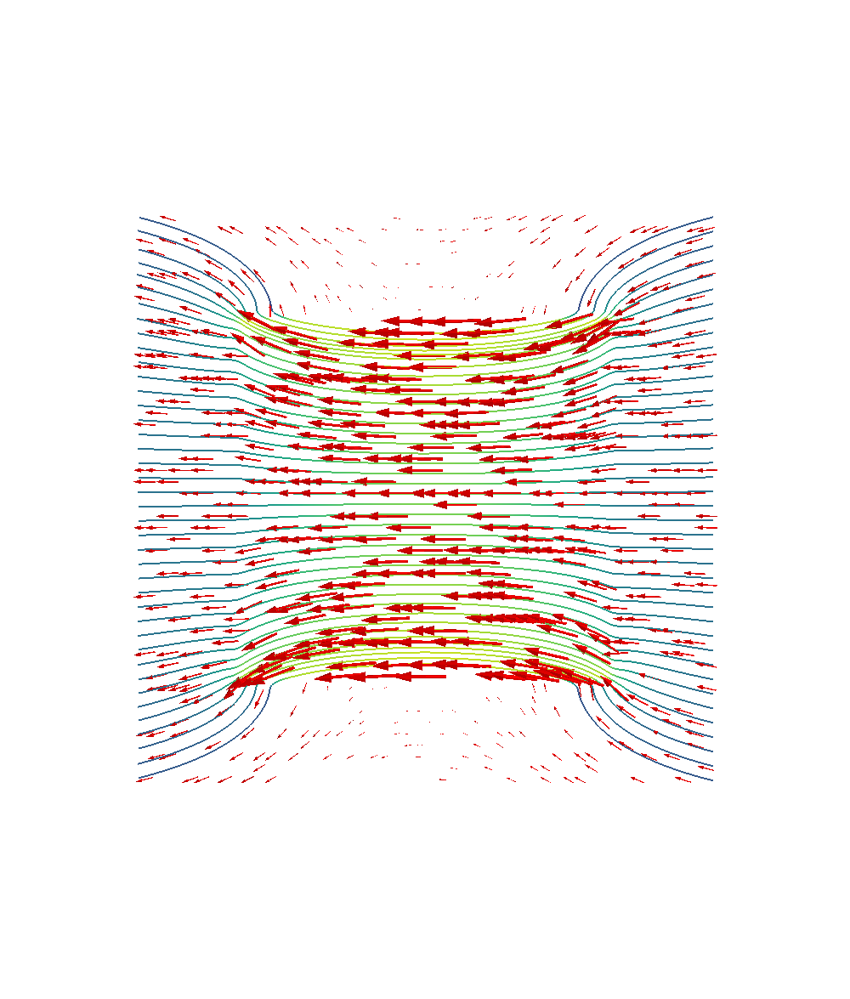
mlab.figure("B field", bgcolor=(1, 1, 1), size=(1000, 1000))
vectors2 = mlab.quiver3d(
*pp.T,
*bplane.T,
color=(1, 0, 0),
scale_mode="vector",
scale_factor=0.02,
mode="arrow"
)
vectors2.glyph.glyph.scale_factor = 0.08
vectors2.glyph.mask_input_points = True
vectors2.glyph.mask_points.random_mode_type = 0
vectors2.glyph.mask_points.on_ratio = 4
vectors2.glyph.glyph_source.glyph_position = "center"
vectors2.scene.z_plus_view()
# Streamline plot for the cube
bplane[:, 2] = 0
vecfield = mlab.pipeline.vector_field(
*pp.T.reshape(3, 50, 50, 1), *bplane.T.reshape(3, 50, 50, 1)
)
vecnorm = mlab.pipeline.extract_vector_norm(vecfield)
streams = []
Nq = 40
q = np.zeros((Nq, 3))
q[:, 1] = np.linspace(-1.5, 1.5, Nq)
q[:, 0] = 1.5
extent = np.array([-1.5, 1.5, -1.5, 1.5, 0, 0])
for qi in q:
stream = mlab.pipeline.streamline(
vecnorm,
seed_scale=0.01,
seedtype="point",
integration_direction="both",
extent=np.array([-1.5, 1.5, -1.5, 1.5, 0, 0]),
colormap="viridis",
)
stream.stream_tracer.initial_integration_step = 0.1
stream.stream_tracer.maximum_propagation = 200.0
stream.seed.widget = stream.seed.widget_list[3]
stream.seed.widget.position = qi
stream.seed.widget.enabled = False # hide the widget itself
streams.append(stream)
Total running time of the script: ( 0 minutes 32.044 seconds)
Estimated memory usage: 2613 MB