Example of spherical harmonics tools and visualization

import numpy as np
from mayavi import mlab
import matplotlib.pyplot as plt

from bfieldtools.sphtools import SphBasis
from bfieldtools import sphtools

# Create basis object for plotting, evaluation of inner products etc.
sph = SphBasis(40)

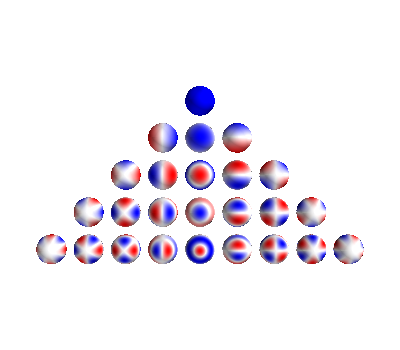
Plot Spherical harmonics Ylms on the sphere Plot Ylms up to l = 4

mlab.figure(bgcolor=(1, 1, 1))
obj = sphtools.plotYlms(sph, lmax=4)

# Plot Ylm with l=3, m=3
mlab.figure(bgcolor=(1, 1, 1))
obj = sphtools.plotYlm(sph, l=3, m=3)

• 
• 

Plot vector spherical harmonics Vlms / Wlms / Xlms on the sphere

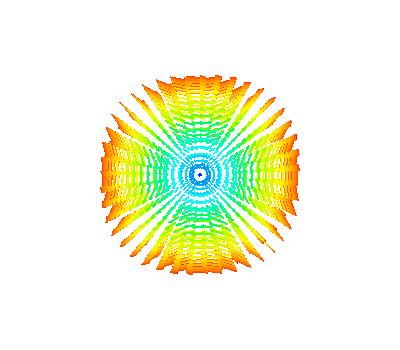
# Plot Vlm with l=2, m=2
mlab.figure(bgcolor=(1, 1, 1))
obj = sphtools.plotVlm(sph, l=2, m=2)
obj.scene.z_plus_view()

# Plot Wlm with the same order and degree, l=2, m=2
mlab.figure(bgcolor=(1, 1, 1))
obj = sphtools.plotWlm(sph, l=2, m=2)
obj.scene.z_plus_view()

# Plot Xlm with the same order and degree, l=2, m=2
mlab.figure(bgcolor=(1, 1, 1))
obj = sphtools.plotXlm(sph, l=2, m=2)
obj.scene.z_plus_view()

• 
• 
• 

Plot fields of vector spherical harmonics Vlms / Wlms on a volume

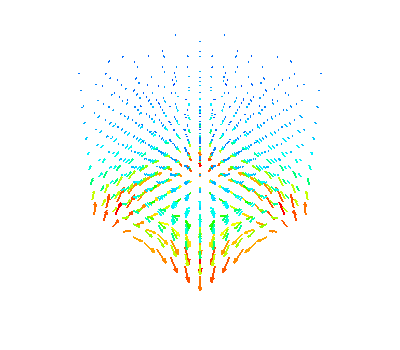
# Plot BVlm with l=2, m=2
offset = np.array((0, 0, 3))  # add offset due to divergence in origin
mlab.figure(bgcolor=(1, 1, 1))
obj = sphtools.plotBVlm_volume(sph, l=2, m=2, lim=1, Np=10, offset=offset)

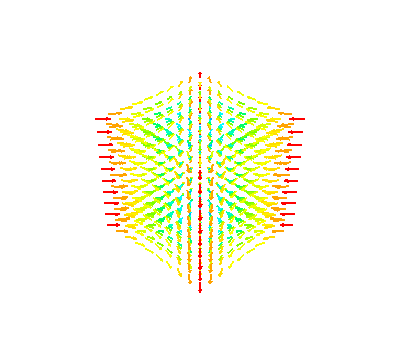
# Plot BWlm with l=2, m=2
offset = np.array((0, 0, 0))  # include origin
mlab.figure(bgcolor=(1, 1, 1))
obj = sphtools.plotBWlm_volume(sph, l=2, m=2, lim=1, Np=10, offset=offset)

• 
• 

Test inner products in quadrature points defined in sph-object

Ylm1 = sphtools.ylm(2, 1, sph.sqp[:, 1], sph.sqp[:, 2])
Ylm2 = sphtools.ylm(2, 0, sph.sqp[:, 1], sph.sqp[:, 2])
print(
    "Inner product between Ylm_20 and Ylm_21 is %f"
    % sph.innerproduct(Ylm1[:, None], Ylm2[:, None])
)
print(
    "Inner product between Ylm_20 and Ylm_20 is %f"
    % sph.innerproduct(Ylm2[:, None], Ylm2[:, None])
)

Vlm1 = sphtools.Vlm(1, 0, sph.sqp[:, 1], sph.sqp[:, 2])
Vlm2 = sphtools.Vlm(2, 0, sph.sqp[:, 1], sph.sqp[:, 2])
print("Inner product between V_10 and V_20 is %f" % sph.innerproduct(Vlm1, Vlm2))
print("Inner product between V_10 and V_10 is %f" % sph.innerproduct(Vlm1, Vlm1))

Wlm1 = sphtools.Wlm(1, 0, sph.sqp[:, 1], sph.sqp[:, 2])
Wlm2 = sphtools.Wlm(2, 0, sph.sqp[:, 1], sph.sqp[:, 2])
print("Inner product between W_10 and W_20 is %f" % sph.innerproduct(Wlm1, Wlm2))
print("Inner product between W_10 and W_10 is %f" % sph.innerproduct(Wlm1, Wlm1))

Xlm1 = sphtools.Xlm(1, 0, sph.sqp[:, 1], sph.sqp[:, 2])
Xlm2 = sphtools.Xlm(2, 0, sph.sqp[:, 1], sph.sqp[:, 2])
print("Inner product between X_10 and X_20 is %f" % sph.innerproduct(Xlm1, Xlm2))
print("Inner product between X_10 and X_10 is %f" % sph.innerproduct(Xlm1, Xlm1))

print("Inner product between W_10 and V_10 is %f" % sph.innerproduct(Wlm1, Vlm1))
print("Inner product between X_10 and V_10 is %f" % sph.innerproduct(Xlm1, Vlm1))
print("Inner product between X_10 and W_10 is %f" % sph.innerproduct(Xlm1, Vlm1))

Out:

Inner product between Ylm_20 and Ylm_21 is 0.000000
Inner product between Ylm_20 and Ylm_20 is 1.000000
Inner product between V_10 and V_20 is 0.000000
Inner product between V_10 and V_10 is 1.000000
Inner product between W_10 and W_20 is -0.000000
Inner product between W_10 and W_10 is 1.000000
Inner product between X_10 and X_20 is -0.000000
Inner product between X_10 and X_10 is 1.000000
Inner product between W_10 and V_10 is 0.000000
Inner product between X_10 and V_10 is 0.000000
Inner product between X_10 and W_10 is 0.000000

Simple example of the calculation of sph spectrum of magnetic field defined on the sphere using the inner product.

# define homogeneous magnetic field along z-axis
B = np.zeros(sph.sqp.shape)
B[:, 2] = sph.qp.points[:, 0] / np.max(sph.qp.points[:, 0])

# add noise
B += 0.1 * np.random.randn(B.shape[0], B.shape[1])

B = sphtools.cartvec2sph(sph.sqp, B)  # transform to spherical coordinates

coeffs = sph.avsphspectra(B, 7)  # calculate spectra of the r**l terms

# Plot the spectra
plt.figure()
plt.semilogy(coeffs ** 2)

Out:

[<matplotlib.lines.Line2D object at 0x7fc4c8a62950>]

Estimated memory usage: 9 MB