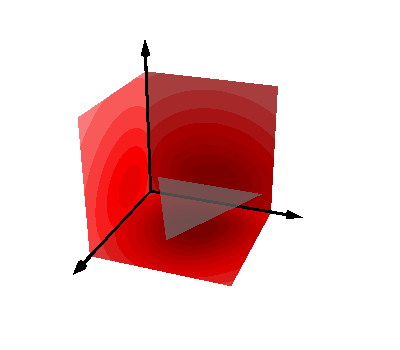
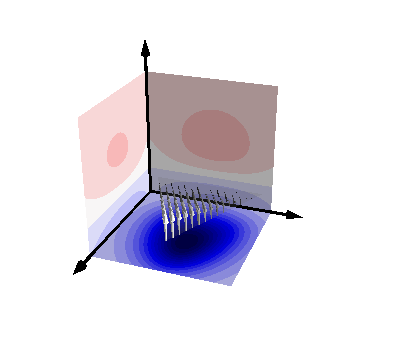
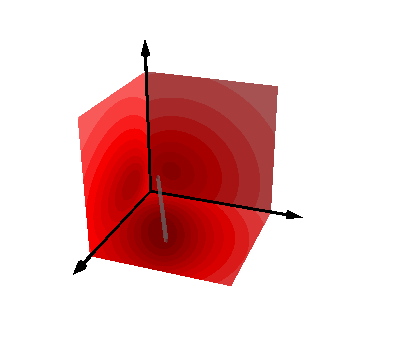
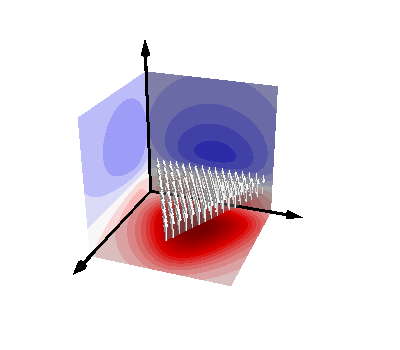
Analytic integrals as scalar fields

import numpy as np
import matplotlib.pyplot as plt
from mayavi import mlab
import trimesh


from bfieldtools.integrals import triangle_potential_uniform
from bfieldtools.integrals import triangle_potential_dipole_linear
from bfieldtools.integrals import gamma0
from bfieldtools.integrals import omega
from bfieldtools.utils import tri_normals_and_areas

%% Create there orthogonal planes

points = np.array([[0, 0, 0], [1, 0.5, 0], [0, 1, 0]]) + 0.15

points[:, 2] += 0.1

tris = np.array([[0, 1, 2]])
p_tris = points[tris]
mesh = trimesh.Trimesh(points, tris, process=False)

# Evaluation points
points2 = np.array([[-0.01, 1, 1], [-0.01, 1, 0], [-0.01, 0, 0], [-0.01, 0, 1]]) * 1.2
tris2 = np.array([[0, 1, 2], [2, 3, 0]])
mesh2 = trimesh.Trimesh(points2, tris2)
for ii in range(7):
    mesh2 = mesh2.subdivide()

points3 = np.array([[1, 1, -0.01], [1, 0, -0.01], [0, 0, -0.01], [0, 1, -0.01]]) * 1.2
mesh3 = trimesh.Trimesh(points3, tris2)
for ii in range(7):
    mesh3 = mesh3.subdivide()

points4 = np.array([[1, -0.01, 1], [1, -0.01, 0], [0, -0.01, 0], [0, -0.01, 1]]) * 1.2
mesh4 = trimesh.Trimesh(points4, tris2)
for ii in range(7):
    mesh4 = mesh4.subdivide()


def plot_axes():
    axes_points = np.zeros((3, 3))
    axes = np.eye(3) * 0.3
    vectors = mlab.quiver3d(*axes_points, *axes, mode="arrow", color=(0, 0, 0))
    vectors.glyph.glyph.scale_factor = 1.5
    vectors.glyph.glyph_source.glyph_source.tip_length = 0.1
    vectors.glyph.glyph_source.glyph_source.tip_radius = 0.03
    vectors.glyph.glyph_source.glyph_source.shaft_radius = 0.01


# Difference vectors
RR2 = mesh2.vertices[:, None, None, :] - p_tris[None, :, :, :]
RR3 = mesh3.vertices[:, None, None, :] - p_tris[None, :, :, :]
RR4 = mesh4.vertices[:, None, None, :] - p_tris[None, :, :, :]

tn, ta = tri_normals_and_areas(points, tris)

for ii, func in enumerate(
    (triangle_potential_uniform, triangle_potential_dipole_linear, gamma0, omega)
):

    mlab.figure(bgcolor=(1, 1, 1))
    # Plot shape and potential
    print(func)
    if ii == 0:
        pot2 = func(RR2, tn)[:, 0]
        pot3 = func(RR3, tn)[:, 0]
        pot4 = func(RR4, tn)[:, 0]
        mlab.triangular_mesh(
            *mesh.vertices.T, mesh.faces, color=(0.5, 0.5, 0.5), opacity=0.7
        )
    if ii == 1:
        pot2 = func(RR2, tn, ta)[:, 0, 1]
        pot3 = func(RR3, tn, ta)[:, 0, 1]
        pot4 = func(RR4, tn, ta)[:, 0, 1]
        mlab.triangular_mesh(
            *mesh.vertices.T, mesh.faces, color=(0.5, 0.5, 0.5), opacity=0.2
        )
        meshq = mesh.copy()
        for jj in range(4):
            meshq = meshq.subdivide()
        u = np.zeros(meshq.vertices.shape)
        r = meshq.vertices
        r2 = np.zeros(r.shape + (3,))
        r2[:, 1] = r
        r2[:, 0] = mesh.vertices[0]
        r2[:, 2] = mesh.vertices[2]
        u[:, 2] = np.linalg.det(r2) / np.linalg.det(mesh.vertices)
        q = mlab.quiver3d(*r.T, *u.T, colormap="gray", mode="arrow")
        q.glyph.glyph.scale_factor = 0.25

    if ii == 2:
        pot2 = func(RR2)[:, 0, 2]
        pot3 = func(RR3)[:, 0, 2]
        pot4 = func(RR4)[:, 0, 2]
        mlab.plot3d(
            *points[0:2].T, color=(0.5, 0.5, 0.5), opacity=0.5, tube_radius=0.02
        )
    if ii == 3:
        pot2 = func(RR2)[:, 0]
        pot3 = func(RR3)[:, 0]
        pot4 = func(RR4)[:, 0]
        mlab.triangular_mesh(
            *mesh.vertices.T, mesh.faces, color=(0.5, 0.5, 0.5), opacity=0.5
        )
        u = np.zeros(meshq.vertices.shape)
        u[:, 2] = 1
        r = meshq.vertices
        q = mlab.quiver3d(*r.T, *u.T, colormap="gray", mode="arrow")
        q.glyph.glyph.scale_factor = 0.2

    plot_axes()

    M = max(max(abs(pot2)), max(abs(pot3)), max(abs(pot4)))
    for m, p in zip((mesh2, mesh3, mesh4), (pot2, pot3, pot4)):
        s = mlab.triangular_mesh(
            *m.vertices.T, m.faces, scalars=p, colormap="seismic", vmin=-M, vmax=M
        )
        s.actor.mapper.interpolate_scalars_before_mapping = True
        s.module_manager.scalar_lut_manager.number_of_colors = 32

    # Move camera a bit
    s.scene.camera.pitch(-2)
    s.scene.camera.azimuth(-25)
    s.scene.camera.elevation(-10)
    s.scene.camera.orthogonalize_view_up()
    s.scene.camera.pitch(1)
    s.scene.camera.orthogonalize_view_up()

• 
• 
• 
• 

Out:

<function triangle_potential_uniform at 0x7f0c1b9f6680>
<function triangle_potential_dipole_linear at 0x7f0c1b9f68c0>
<function gamma0 at 0x7f0c1b9f6320>
<function omega at 0x7f0c1b9f63b0>

Estimated memory usage: 12 MB