Inductance computation time and memory benchmark

Benchmark for inductance matrix computation, used to set auto-chunking.

• 
• 

Out:

Computing self-inductance matrix using rough quadrature (degree=2).              For higher accuracy, set quad_degree to 4 or more.
Computing triangle-coupling matrix
Computing self-inductance matrix using rough quadrature (degree=2).              For higher accuracy, set quad_degree to 4 or more.
Computing triangle-coupling matrix
Computing self-inductance matrix using rough quadrature (degree=2).              For higher accuracy, set quad_degree to 4 or more.
Computing triangle-coupling matrix
Computing self-inductance matrix using rough quadrature (degree=2).              For higher accuracy, set quad_degree to 4 or more.
Computing triangle-coupling matrix
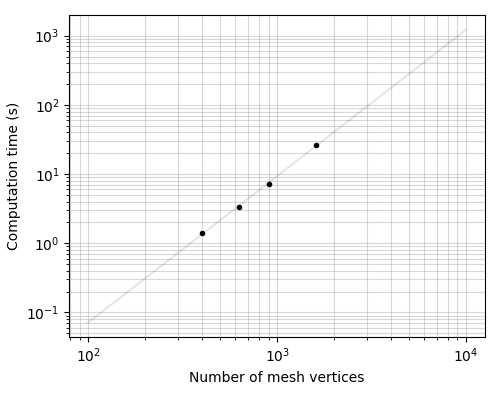
Fit:
t = 0.000004 n**2.12
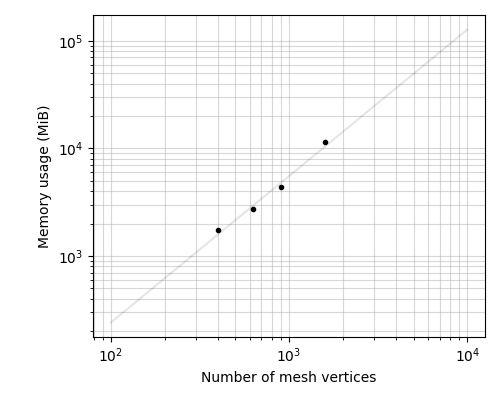
Fit:
memory = 0.456410 n**1.36

SAVE = False


import numpy as np
import matplotlib.pyplot as plt
import trimesh

from memory_profiler import memory_usage


def MakeFacesVectorized1(Nr, Nc):

    out = np.empty((Nr - 1, Nc - 1, 2, 3), dtype=int)

    r = np.arange(Nr * Nc).reshape(Nr, Nc)

    out[:, :, 0, 0] = r[:-1, :-1]
    out[:, :, 1, 0] = r[:-1, 1:]
    out[:, :, 0, 1] = r[:-1, 1:]

    out[:, :, 1, 1] = r[1:, 1:]
    out[:, :, :, 2] = r[1:, :-1, None]

    out.shape = (-1, 3)
    return out


Nr = 50
Nc = 50
d = 1


from bfieldtools.mesh_impedance import self_inductance_matrix
import time

N_vertices = []
comp_time = []
mem_use = []


# NE = [20, 30, 40, 60]#, 80]
NE = [20, 25, 30, 40]
for Ne in NE:
    x0 = np.arange(Ne) * d
    y0 = np.arange(Ne) * d
    X, Y = np.meshgrid(x0, y0)
    Z = np.zeros_like(X)

    vertices = np.array([X.flatten(), Y.flatten(), Z.flatten()]).T
    faces = MakeFacesVectorized1(Ne, Ne)

    mesh = trimesh.Trimesh(vertices=vertices, faces=faces)

    N_vertices.append(mesh.vertices.shape[0])
    Nchunks = 1

    #    if mesh.vertices.shape[0] > 3000:
    #        Nchunks=3
    #    if mesh.vertices.shape[0] > 6000:
    #        Nchunks=5
    start_t = time.time()
    mem_use.append(
        np.max(
            memory_usage(
                (
                    self_inductance_matrix,
                    (mesh,),
                    {"Nchunks": Nchunks, "quad_degree": 2},
                )
            )
        )
    )

    comp_time.append(time.time() - start_t)


fig, ax = plt.subplots(nrows=1, ncols=1, figsize=(5, 4))
ax.loglog(N_vertices, comp_time, ".k")
ax.set_xlabel("Number of mesh vertices")
# plt.legend()
ax.set_ylabel("Computation time (s)")
#
# ax.spines['top'].set_visible(False)
# ax.spines['right'].set_visible(False)

ax.grid(which="both", alpha=0.5)

fig.tight_layout()

coefs = np.polyfit(np.log(N_vertices), np.log(comp_time), 1)


N = np.linspace(100, 10000, 200)
T = np.exp(coefs[1]) * N ** coefs[0]

ax.loglog(N, T, "-k", alpha=0.1)
print("Fit:")
print("t = %.6f n**%.2f" % (np.exp(coefs[1]), coefs[0]))

if SAVE:
    fig.savefig("inductance_computation_time.pdf")


fig, ax = plt.subplots(nrows=1, ncols=1, figsize=(5, 4))
ax.loglog(N_vertices, mem_use, ".k")
ax.set_xlabel("Number of mesh vertices")
# plt.legend()
ax.set_ylabel("Memory usage (MiB)")
#
# ax.spines['top'].set_visible(False)
# ax.spines['right'].set_visible(False)

ax.grid(which="both", alpha=0.5)

fig.tight_layout()

mem_coefs = np.polyfit(np.log(N_vertices), np.log(mem_use), 1)


MEM = np.exp(mem_coefs[1]) * N ** mem_coefs[0]

ax.loglog(N, MEM, "-k", alpha=0.1)
print("Fit:")
print("memory = %.6f n**%.2f" % (np.exp(mem_coefs[1]), mem_coefs[0]))

if SAVE:
    fig.savefig("inductance_memory_usage.pdf")