Validation of Laplacian using spherical harmonics

Study the eigenvalue spectrum of the discretize laplace-beltrami operator on a spherical mesh. Compare the spectrum to analytical solution.

import numpy as np
from bfieldtools.mesh_calculus import mass_matrix, laplacian_matrix
from bfieldtools.utils import load_example_mesh
from scipy.sparse.linalg import eigsh
import matplotlib.pyplot as plt
import trimesh

# This is icosphere(4)?
# mesh = load_example_mesh("unit_sphere")
# The test is faster with a smaller number of vertices
mesh = trimesh.creation.icosphere(3)

Nvals = 150
uu1 = []
vv1 = []
M = mass_matrix(mesh)

# for q in range(4):
L = laplacian_matrix(mesh)
uu, vv = eigsh(-L, Nvals, M, which="SM")
uu1.append(uu)
vv1.append(vv)

"""
 Spherical harmonics are the eigenfunctions of the LB operator
 The correct eigenvalues are l*(l+1)
"""
R = np.linalg.norm(mesh.vertices[mesh.faces].mean(axis=1), axis=-1).mean()
ll = np.array([l for l in range(20) for m in range(-l, l + 1)])
ll = ll[:Nvals]
evals = ll * (ll + 1)

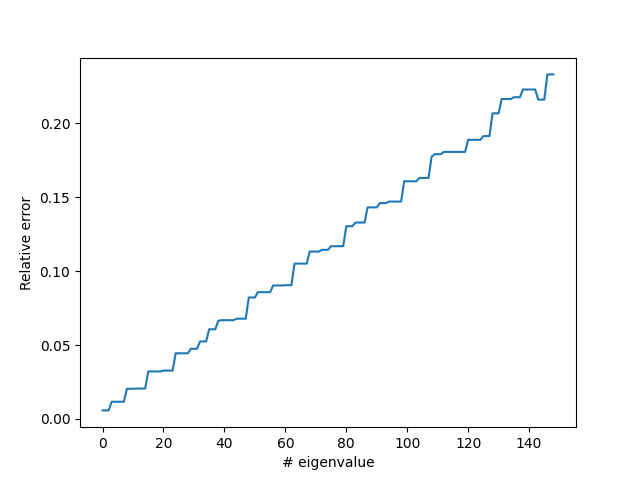
plt.plot(evals, ‘k’)

for u in uu1:
    plt.plot(abs(evals[1:] - u[1:]) / evals[1:], "-")

plt.xlabel("# eigenvalue")
plt.ylabel("Relative error")

Out:

Text(0, 0.5, 'Relative error')

from bfieldtools.utils import MeshProjection
from bfieldtools.sphtools import ylm
from bfieldtools.sphtools import cartesian2spherical

ylm_on_hats = []
i1 = 0
vv1_projs = np.zeros((len(vv1), vv1[0].shape[1]))
mp = MeshProjection(mesh, 4)

# N < L*(L+2)
for l in range(0, 13):
    i0 = i1
    print(f"l={l}")
    for m in range(-l, l + 1):

        def func(r):
            sphcoords = cartesian2spherical(r)
            return ylm(l, m, sphcoords[:, 1], sphcoords[:, 2])

        ylm_on_hats.append(mp.hatfunc_innerproducts(func))
        i1 += 1
    for ii, vv in enumerate(vv1):
        # Project self-inductance eigenfunctions to l-subspace
        p = np.sum((np.array(ylm_on_hats[i0:i1]) @ vv[:, i0:i1]) ** 2, axis=0)
        vv1_projs[ii, i0:i1] = p

Out:

l=0
l=1
l=2
l=3
l=4
l=5
l=6
l=7
l=8
l=9
l=10
l=11
l=12

"""
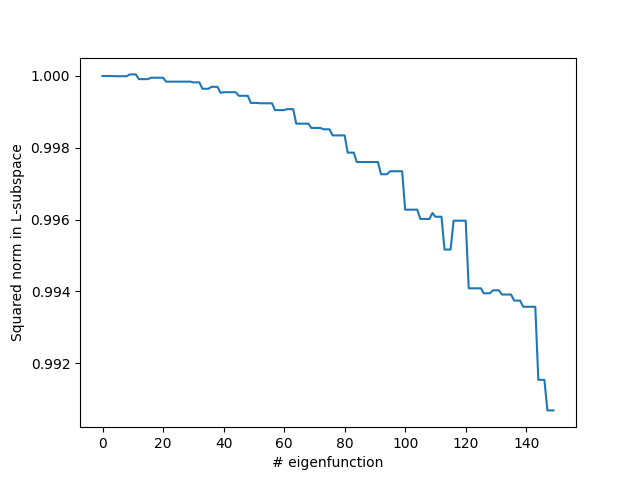
Plot the norm of a projection of the eigenfunctions into the L-subspaces
corresponding to the same degenerate eigenvalue.
The correct values should be 1, if they are less than one the eigenfunctions
span also to other subspaces
"""
plt.figure()
eff_R2 = np.sum(mesh.area_faces) / (4 * np.pi)
plt.plot(np.sqrt(vv1_projs.T / eff_R2), "-")

plt.xlabel("# eigenfunction")
plt.ylabel("Squared norm in L-subspace")

Out:

Text(0, 0.5, 'Squared norm in L-subspace')